
Kafli 5 • Líkur og talningarfræði
51
5.64
Alls eru 28 nemendur í 9. A. Tíu nemendanna eiga hund, átta nemendur eiga kött
og 16 nemendur eiga hvorki hund né kött.
a
Teiknaðu Vennmyndina á spássíunni upp og finndu hve margir
nemendur eru í hvoru mengi.
b
Hvað einkennir nemendurna í sniðmenginu?
c
Einn nemendanna er valinn af handahófi
til að ræða við skólastjórann.
Hversu líklegt er að þetta verði nemandi sem á
• bæði hund og kött?
• bara hund?
• hvorki hund né kött?
5.65
Hér eru tvö mengi:
A
= {2, 4, 6, 8, 10, 12}
B
= {0, 1, 2, 3, 4, 5}
a
Skráðu
A
∪
B
.
b
Skráðu
A
∩
B
.
5.66
Hér eru tvö mengi:
A
er mengi allra oddatalna milli 0 og 20.
B
er mengi allra frumtalna milli 10 og 20.
a
Skráðu
A
∪
B
.
b
Skráðu
A
∩
B
.
5.67
Þú dregur eina heila tölu af talnabilinu 10–20 að báðum
tölunum meðtöldum. Skráðu eftirfarandi mengi og fyllimengi:
a
A
er slétt tala.
b
B
er frumtala.
c
C
er tala sem er stærri en 15.
5.68
A
er mengi allra heilla talna frá 0 til 100 og
B
er mengi allra frumtalna
milli 0 og 100. Hvaða fullyrðingar eru sannar?
a
Talan 17 er í sniðmenginu.
b
A
⊂
B
Köttur
Hundur
c
B
⊂
A
d
B
=
A
∩
B
e
B
=
A
\
B
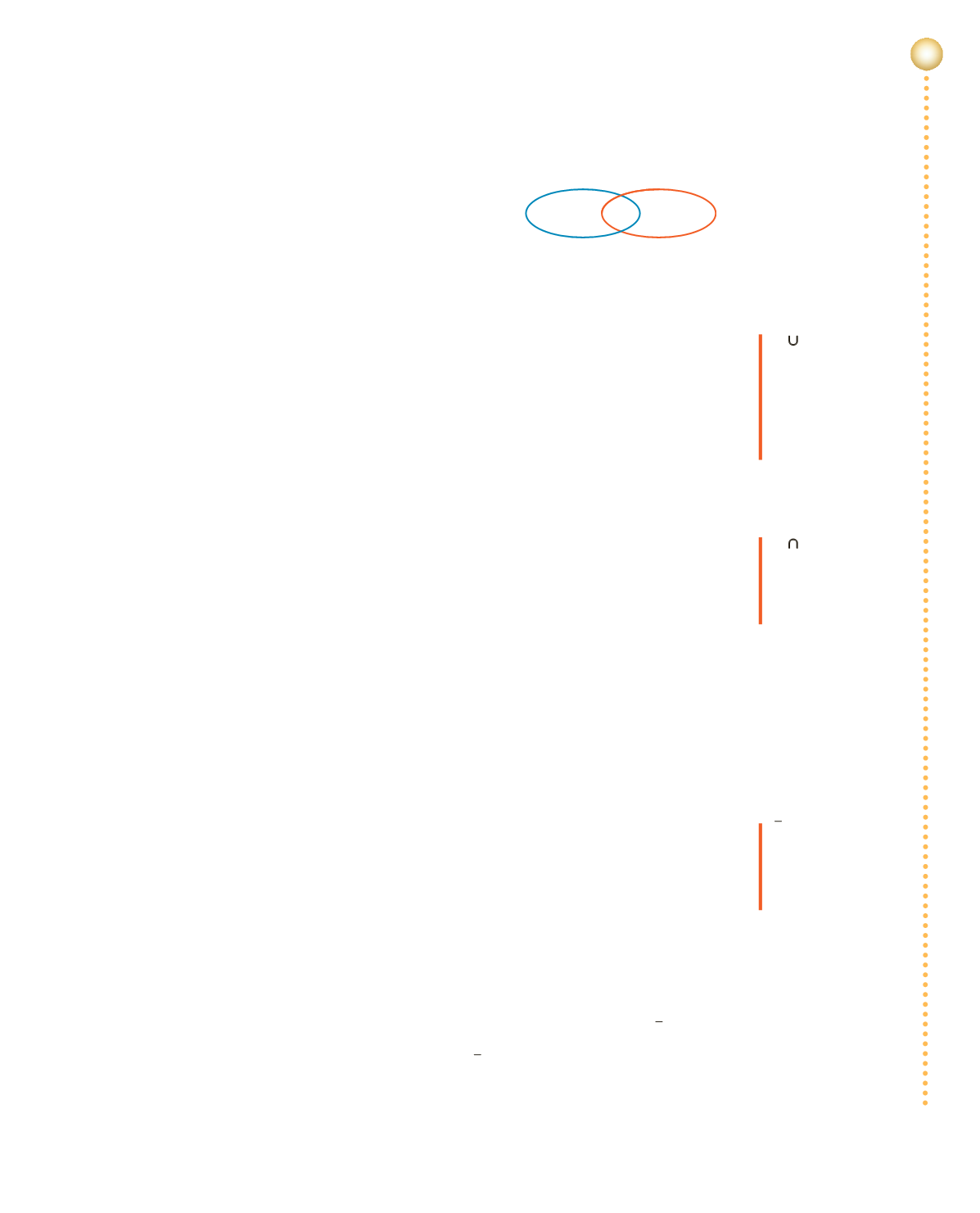
A
∪
B
er sammengi
A og B og er lesið:
A sam B.
Í því eru öll stök í A,
öll stök í B og
öll stök sem eru
bæði í A og B.
A
∩
B
er sniðmengi
A og B og er lesið:
A snið B.
Í því eru stök sem
eru bæði í A og B.
A
táknar fyllimengi
A en það er mengi
þeirra staka í
grunnmenginu
sem eru ekki í A.
















