
Skali 3B
38
Í stuttu máli
Þú átt að geta
Dæmi
Tillögur að lausnum
þekkt annars stigs föll
Hvað föll hér fyrir neðan
eru annars stigs föll?
a
f
(
x
) =
x
2
+ 4
_______
2
b
g
(
x
) =
x
2
1
_______
x
2
c
h
(
x
) =
3
_______
x
2
+ 1
a
f
er annars stigs fall af því að hægt er
að umrita það í
f
(
x
) =
1
___
2
x
2
+ 2
b
g
er ekki annars stigs fall af því að
x
kemur fyrir í nefnaranum.
c
h
er ekki annars stigs fall af því að
x
2
kemur fyrir í nefnaranum.
teiknað megindrætti
fleygboga út frá
fallstæðunni
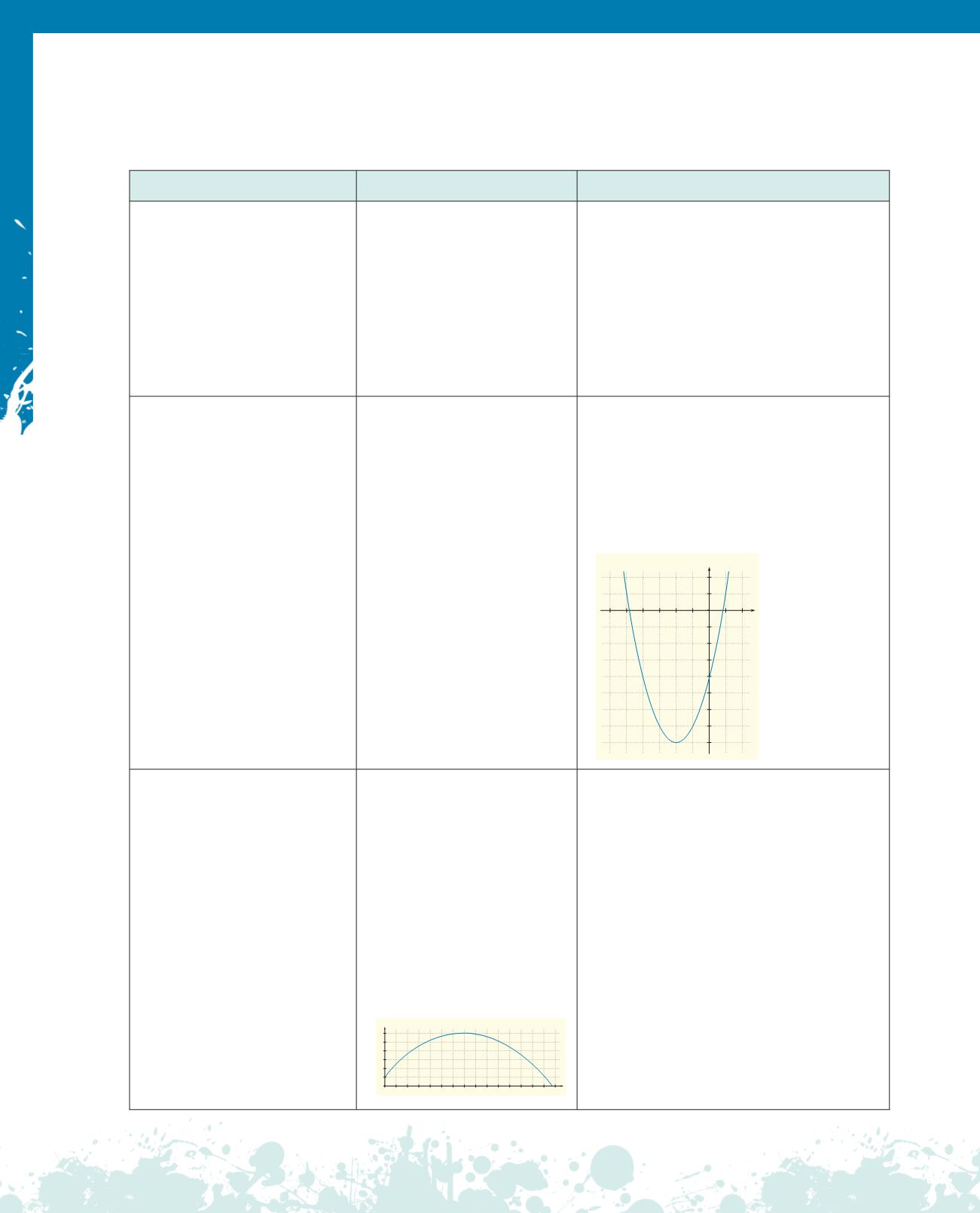
Skýrðu hvernig graf
f
(
x
) = (
x
+ 2)
2
8
lítur út og teiknaðu
megindrætti grafsins.
Graf
f
er fleygbogi með botnpunkt í
(2, 8). Graf
f
hefur hliðrast um átta
einingar niður og tvær einingar til vinstri
miðað við grafið af
x
2
.
Fyrst
f
(0) = 4, sker grafið
y
-ásinn í
(0, 4). Vegna samhverfu er (4, 4)
punktur á grafinu, sem lítur svona út:
ákvarðað topp- eða
botnpunkt fleygboga
a
Finndu topppunkt
fleygbogans
f
(
x
) = (
x
1)
2
+ 2
b
Sýndu að fallið í a má
einnig rita
f
(
x
) =
x
2
+ 2
x
+ 1
c
Bolti fer eftir brautinni
sem sýnd er hér fyrir
neðan. Hve hátt fer
boltinn?
a
Fleygboginn sem táknar
f
, hefur
hliðrast um eina einingu til hægri
og tvær einingar upp miðað við
x
2
.
Þar að auki hefur hann speglast um
x-ásinn. Þess vegna hefur hann
topppunkt í (1, 2).
b
f
(
x
) = (
x
1)
2
+ 2
= (
x
2
2
x
+ 1) + 2
=
x
2
+ 2
x
1 + 2
=
x
2
+ 2
x
+ 1
c
Boltinn fer í 6 m hæð yfir völlinn.
2
1
–1
–1 0
0
1 2
y
−ás
x
−ás
–2 –3 –4 –5
–2
–3
–4
–5
–6
–7
–8
–6
g
Hæð ím
6
5
4
3
2
1
30 28 26 24 22 20 18 16 14 12 10 8 6 4 2 0
0
Fjarlægðeftir vellinum,m
















