
Kafli 4 • Föll
17
Lárétt og lóðrétt hliðrun
Ef við drögum saman það sem við gerðum til að fara frá
f
í
h
og í
g
,
með láréttri hliðrun og lóðréttri hliðrun fáum við fallið
k
(
x
) = (
x
2)
2
4
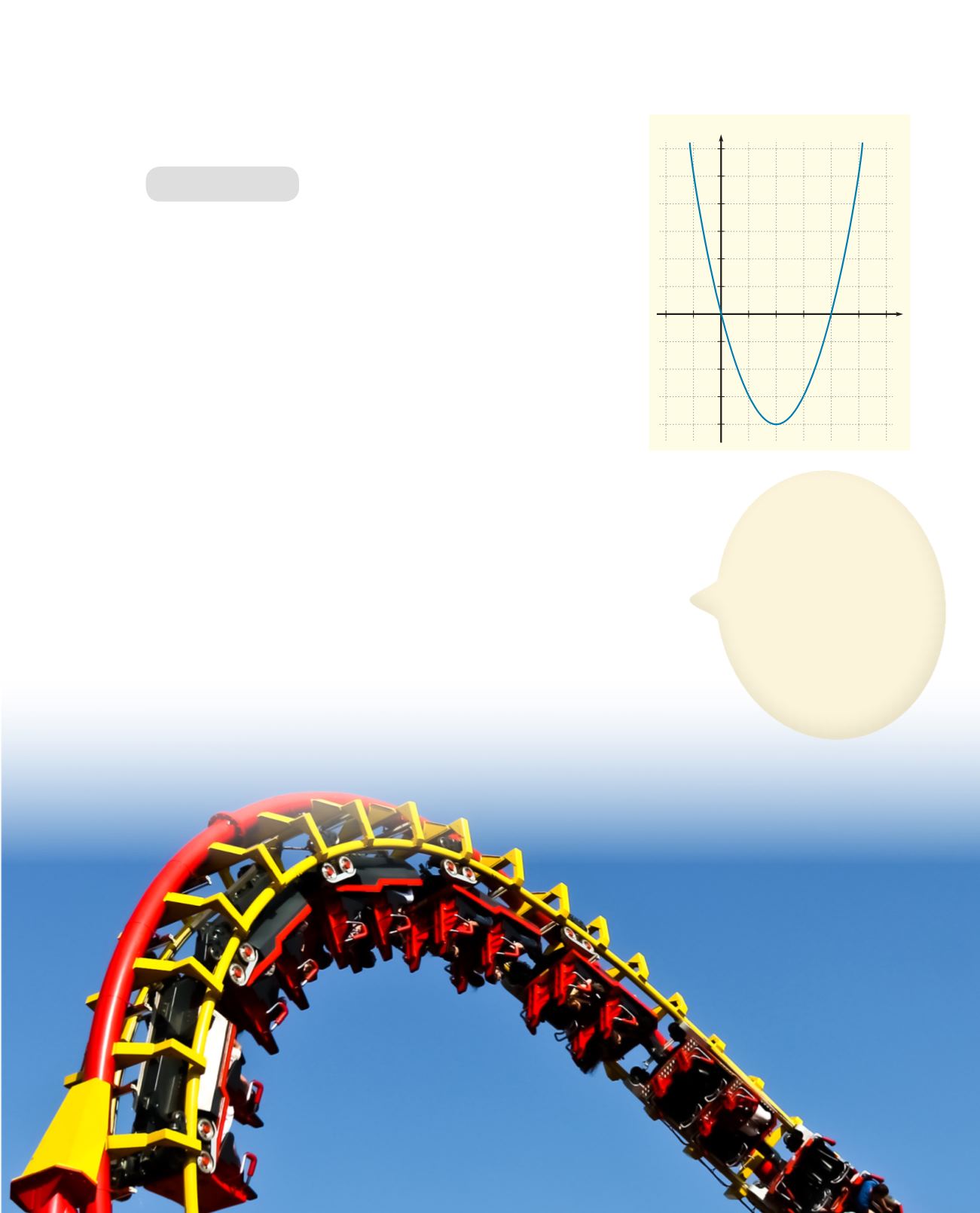
Hér hefur
f
verið hliðrað um tvær einingar til hægri og fjórar
einingar niður á við. Botnpunkturinn hefur flust frá (0, 0) til
(2, 4), og grafið sker
x
-ásinn í punktunum (0, 0) og (4, 0).
Sjá grafið til hægri.
Ef við margföldum upp úr sviganum og drögum saman sjáum við
að það er líka hægt að rita
k
k
(
x
) = (
x
2)
2
4 =
x
2
4
x
+ 4 4 =
x
2
4
x
Ef við þáttum
k
fáum við
k
(
x
) =
x
(
x
4).
Þá sjáum við að
k
(
x
) = 0 þegar
x
= 0 og
x
= 4.
4.12
Þú skalt nota teikniforrit við þetta verkefni.
a
Búðu til tvær rennistikur
a
og
b
sem geta tekið gildi frá 5 til 5.
Teiknaðu graf fallsins
h
(
x
) =
f
(
x
a
) +
b
= (
x
a
)
2
+
b
.
b
Láttu
a
og
b
taka breytileg gildi og lýstu því hvernig grafið breytist.
c
Búðu til setningu um hvernig fallið
f
(
x
) =
x
2
breytist þegar þú dregur
tölu frá eða bætir tölu við
x
og dregur um leið tölu frá eða bætir tölu
við
f
(
x
).
Látum fall
f
vera
f
(
x
) =
x
2
. Þá er
f
(
x
–
a
) +
b
= (
x
–
a
)
2
+
b
hliðrun grafsins um
a
einingar til hægri og
b
einingar upp eftir
y
-ásnum
ef
a
og
b
eru jákvæðar tölur.
Ef
a
er neikvæð tala hliðrast
grafið til vinstri og
ef
b
er neikvæð tala
hliðrast það
niður á við.
5
4
3
2
1
–1
–2 –1 0
0
1 2 3 4
y
−ás
x
−ás
5
6
6
–2
3
-4
5
4
3
2
1
–1
–4 –3 –2 –1 0
0
1 2 3 4
y
−akse
x
−akse
5
6
6
–2
3
-4
















