
Skali 3B
14
Graf
f
(
x
) =
x
2
og hliðranir grafsins
f
(
x
) =
x
2
Einfaldasta annars stigs fallið er
f
(
x
) =
x
2
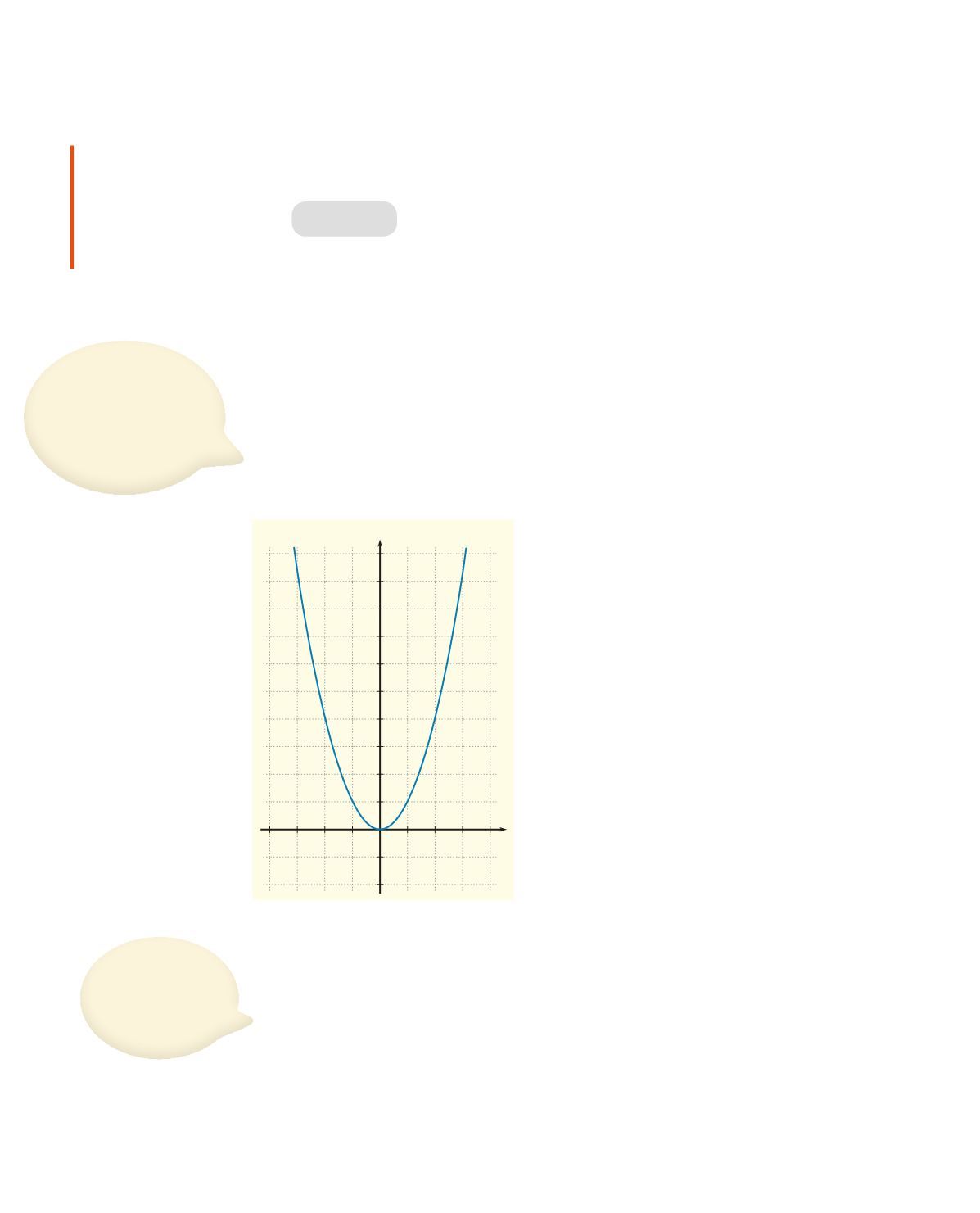
Áður en við teiknum grafið skulum við reyna að skilja hvernig það lítur út.
Fallstæðan sýnir að hefja á
x
-gildin upp í annað veldi. Þá vitum við að svarið
er alltaf jákvætt. Eina undantekningin er
x
= 0 en þá er fallgildið líka 0. Grafið
gengur í gegnum upphafspunktinn (0, 0) og liggur ofan við
x
-ásinn.
Ennfremur sjáum við að við fáum sama fallgildi hvort sem
x
er jákvætt eða
neikvætt þegar tölurnar hafa sama tölugildi.
Til dæmis er
f
(1) = 1
2
= 1 og
f
(1) = (1)
2
= 1.
Á sama hátt er
f
(2) =
f
(2) = 4.
Við sjáum að
f
(
a
) =
f
(
a
) =
a
2
fyrir öll gildi á
a
.
Það þýðir að fallgildin eru hin sömu
fyrir hver tvö gildi sem eru jafnlangt
frá
y
-ásnum hvort sínu megin við 0.
Þá hlýtur grafið að vera samhverft um
y
-ásinn og ganga í gegnum upphafspunkt.
Það verður brattara eftir því sem
x
stækkar af því að
x
er hafið upp
í annað veldi.
Til vinstri er grafið teiknað í teikniforriti.
4.9
a
Teiknið graf
f
(
x
) =
x
2
. Veljið heiltölugildi frá 4 til 4.
b
Hvert er fallgildi
f
þegar
x
= 10?
c
Hvaða
x
-gildi gefa fallgildið 169?
Tölugildi tölu
,
þegar talað er um
tölugildi tölu er litið
fram hjá formerkinu.
Við skráum
|3| = 3 og |–3| = 3.
Fallgildin eru
gildin á y-ásnum.
5
4
3
2
1
–1
–2
–4 –3 –2 –1 0
0
1 2 3 4
y
−ás
6
7
8
9
10
x
−ás
Annars stigs fall
,
fall á forminu
f
(
x
)=
ax
2
+
bx
+
c
,
þar sem
a
,
b
og
c
eru fastar (tölur),
og
x
er breyta,
a
er ekki núll.
















