
Skali 3B
16
Lóðrétt hliðrun
Hvernig hliðrast grafið ef við bætum tölu við eða drögum tölu frá öllum fallgildum?
Lítum á fallið
g
(
x
) =
x
2
4
Við sjáum að
g
(
x
) =
f
(
x
) 4. Til að finna fallgildi
g
fyrir tiltekin
x
-gildi getum við
tekið samsvarandi fallgildi
f
og dregið 4 frá. Það hlýtur að þýða að grafið flyst fjórar
einingar niður fyrir
y
-ásinn og að það er áfram samhverft um
y
-ásinn.
Botnpunkturinn
verður (0, 4).
Þú hefur lært samokaregluna og þá sérðu kannski að það má einnig rita
g
á forminu
g
(
x
) = (
x
2)(
x
+ 2)
Nú sjáum við að
g
(
x
) = 0 þegar
x
= 2 og
x
= 2, og þá sker grafið
x
-ásinn í
punktunum (2, 0) og (2, 0). Þeir samsvara punktunum (2, 4) og (2, 4) á grafi
f
.
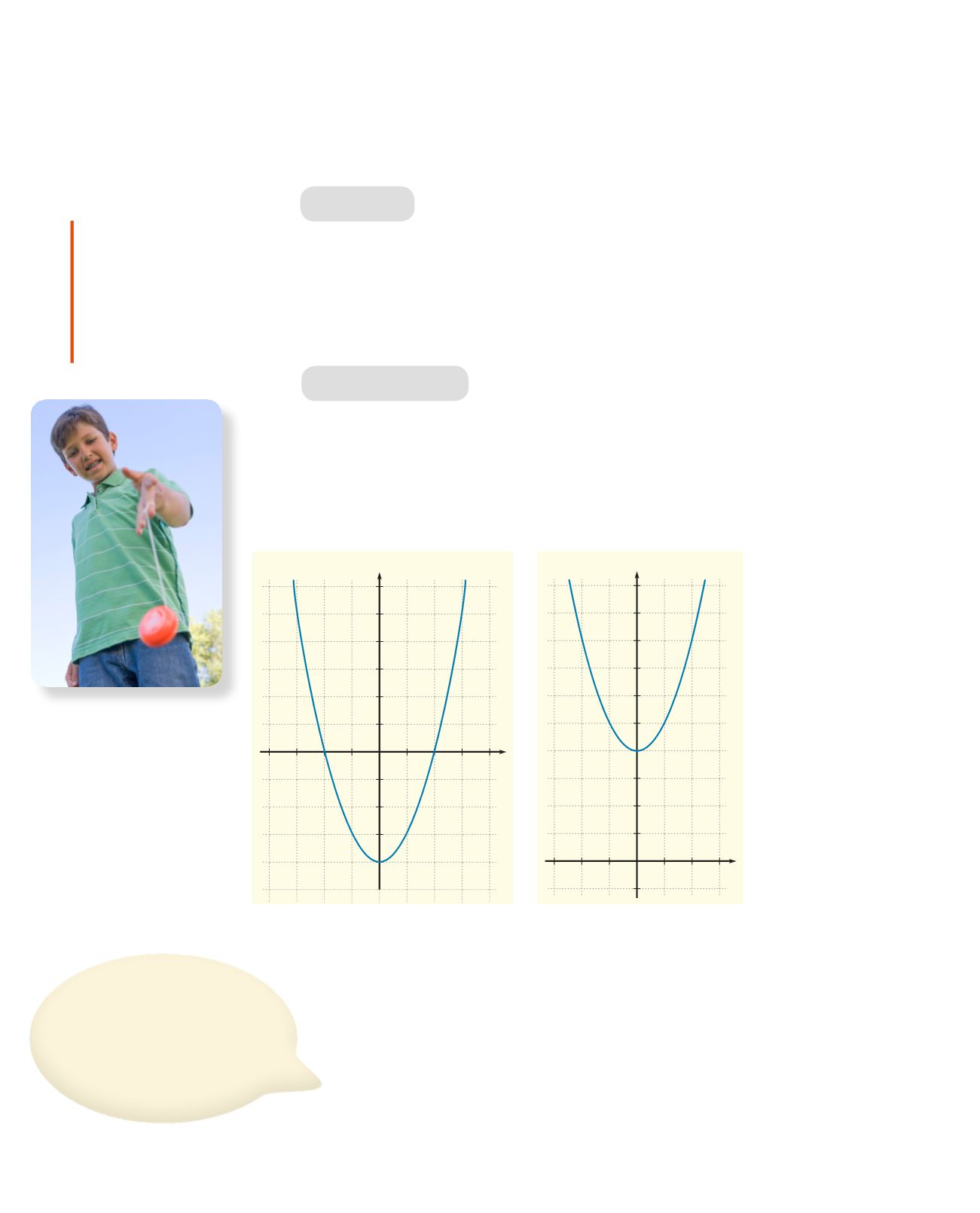
Sjá grafið vinstra megin hér fyrir neðan.
Á sama hátt hliðrast graf
f
(
x
) + 4 =
x
2
+ 4 fjórar einingar upp eftir
y
-ásnum.
Þetta graf sker
x
-ásinn hvergi, sjá grafið hér að neðan til hægri.
4.11
Þú skalt nota teikniforrit í þessu verkefni.
a
Búðu til rennistiku b sem getur tekið gildi frá 5 til 5.
Teiknaðu graf fallsins
g
(
x
) =
f
(
x
) +
b
=
x
2
+
b
.
b
Breyttu
b
-gildunum og lýstu því hvað verður um grafið.
c
Búðu til setningu um hvernig fallið
f
(
x
) =
x
2
breytist
þegar þú dregur tölu frá eða bætir tölu við
f
(
x
).
Látum fallið
f
vera
f
(
x
) =
x
2
. Þá er
f
(
x
) +
b
=
x
2
+
b
hliðrun grafsins um
b
einingar
eftir
y
-ásnum. Ef
b
er neikvæð
tala hliðrast grafið niður á við, og
ef
b
er jákvæð tala hliðrast það
upp á við.
Botnpunktur
er punktur sem
hefur lægra
fallgildi en allir
punktarnir í
nágrenninu,
sama og lággildis-
punktur.
5
4
3
2
1
–1
–4 –3 –2 –1 0
0
1 2 3 4
y
−ás
x
−ás
6
–2
–3
–4
5
4
3
2
1
–1
–3 –2 –1 0
0
1 2 3
y
−ás
x
−ás
6
7
8
9
10
g
(
x
) =
x
2
4
f
(
x
) + 4 =
x
2
+ 4
















