
Sýnidæmi 2
Kafli 4 • Föll
11
Bolta er spyrnt upp í loft. Braut boltans má lýsa með jöfnunni
f
(
x
) = 3,3
x
2
+ 10
x
þar sem
f
(
x
) er hæðin yfir vellinum, og
x
er fjarlægðin frá upphafspunkti
út eftir vellinum.
a
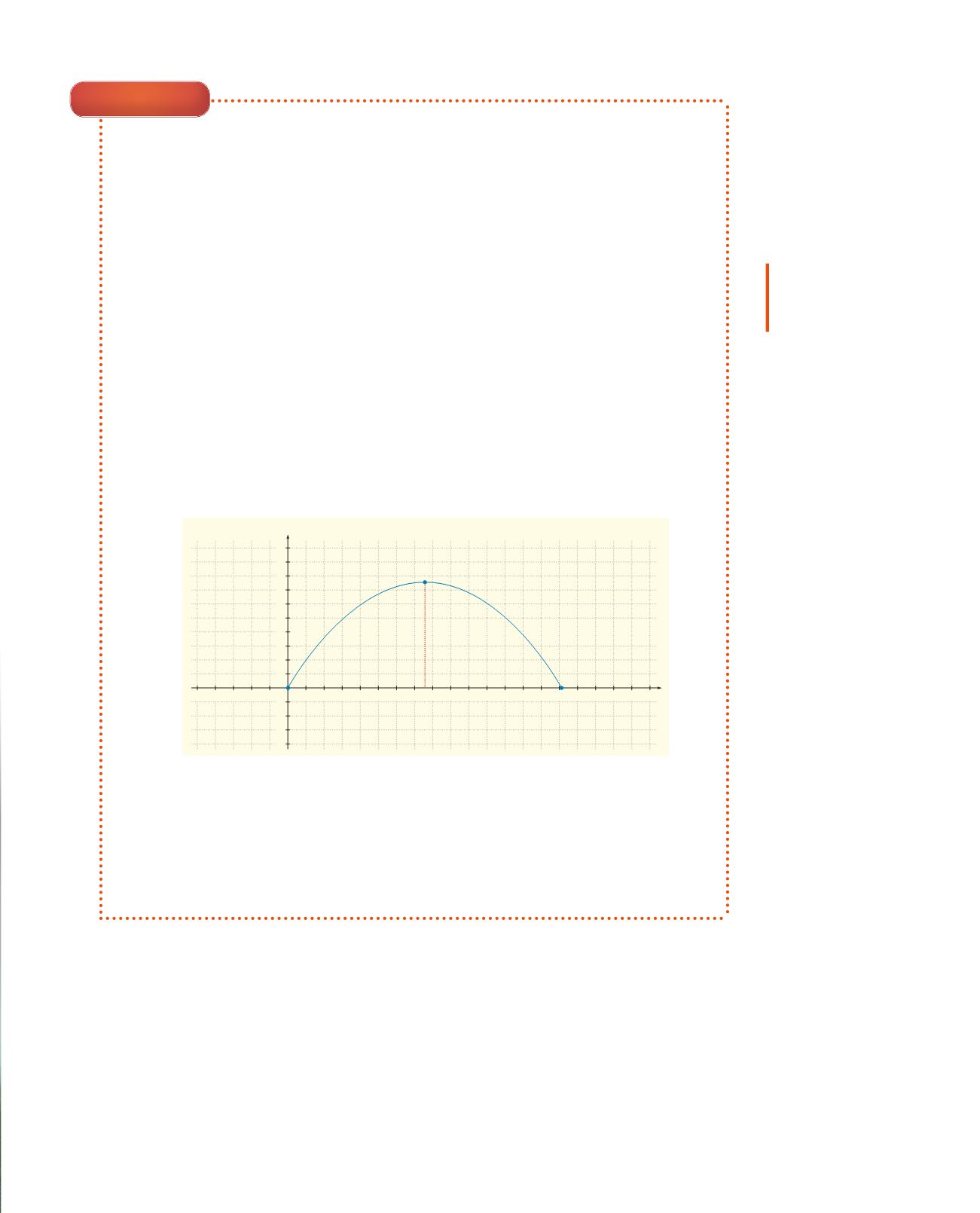
Teiknaðu graf
f
með teikniforriti.
b
Finndu hæsta punkt brautar boltans.
c
Hve langt út eftir vellinum er boltanum spyrnt?
Tillaga að lausn
a
Teiknaðu grafið fyrst án takmarkana. Teiknaðu síðan nýtt graf
þannig að braut boltans fari ekki niður fyrir yfirborð vallarins.
Gerðu fyrra grafið ósýnilegt.
b
Þú getur notað skipunina „
Útgildi
“ til að finna hæsta punktinn.
C (1.52,7.58)
7,58 m
A
B (3.03,0)
Hæð í m
10
9
8
7
6
5
4
3
2
1
-1
-2
-3
-4
Fjarlægð eftir vellinum, m
4 3,8 3,6 3,4 3,2 3 2,8 2,6 2,4 2,2 2 1,8 1,6 1,4 1,2 1 0,8 0,6 0,4 0,2 0
0
-0,2
-0,4
-0,6
-0,8 1
Boltinn er í hæsta punkti þegar hann er um það bil 1,5 m frá
upphafspunkti, mælt út eftir vellinum. Hann er þá í um það bil
7,6 m hæð yfir vellinum.
c
Grafið sker
x
-ásinn í punktinum (3,03, 0). Það þýðir að boltanum
er spyrnt um það bil 3 m, mælt út eftir vellinum.
Dæmið sýnir að graf falls með
x
2
-lið lítur allt öðru vísi út en graf línulegs falls.
Bogaformið er einkennandi fyrir slík gröf. Við nefndum það
fleygboga
.
Útgildi
er samheiti
lággildis og hágildis.
Er notað í teikni-
forritum.
















