
Sýnidæmi 3
Skali 3A
56
Pýþagórasarreglan og sérstakir þríhyrningar
Í rétthyrndum þríhyrningum þar sem hvössu hornin hafa ákveðin mál er hægt
að nota Pýþagórasarregluna ásamt öðrum eiginleikum þríhyrninganna.
2.10
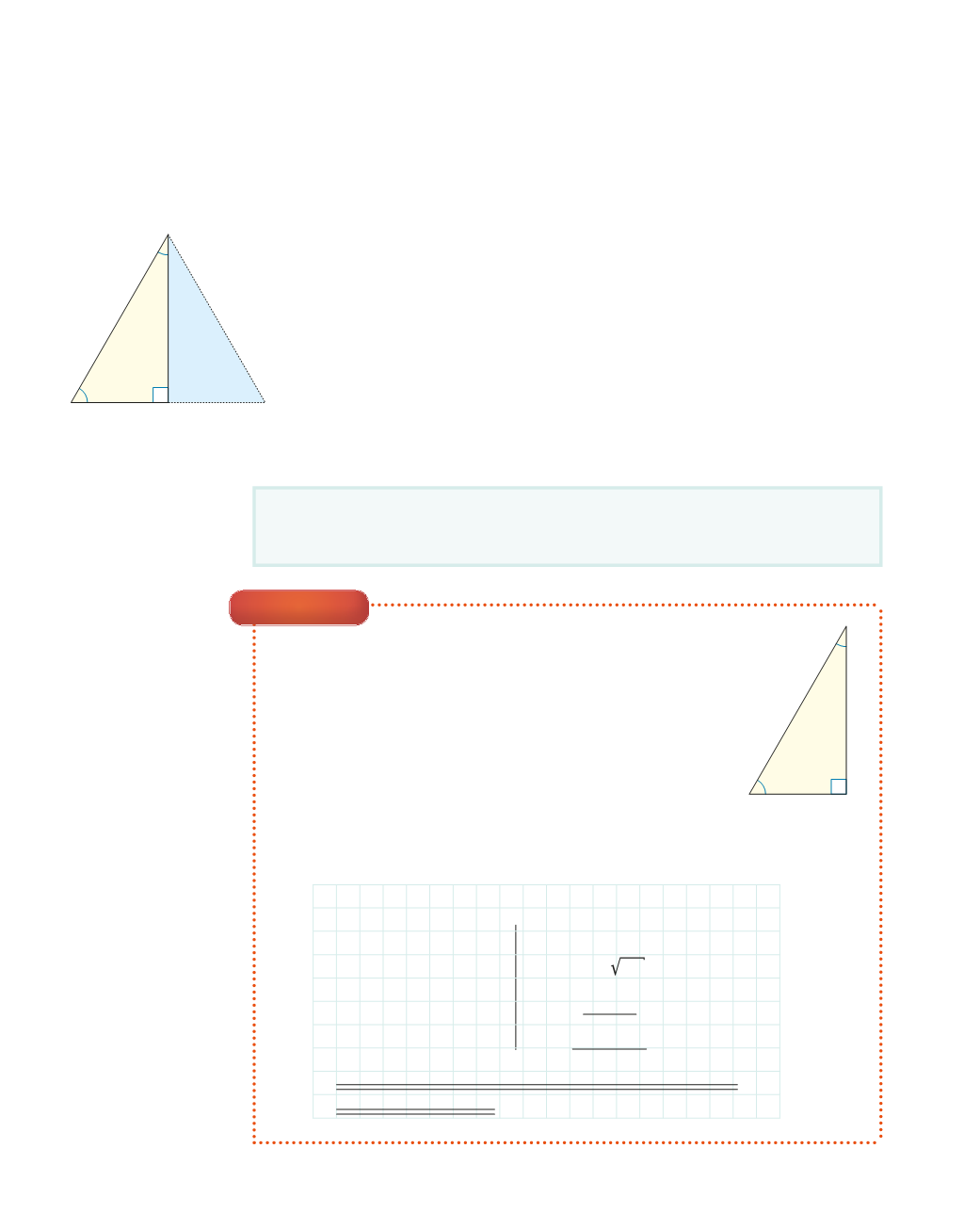
Skoðaðu myndina til vinstri. Lóðrétta strikið skiptir stóra þríhyrningnum
í tvo jafn stóra hluta.
a
Hvers konar þríhyrningur er stóri þríhyrningurinn?
b
Hvers konar þríhyrningur er blái þríhyrningurinn?
c
Hve löng er styttri skammhliðin í bláa þríhyrningnum þegar hliðarlengdin
í stóra þríhyrningnum er 10 cm?
d
Hve löng er hliðin í stóra þríhyrningnum þegar styttri skammhlið bláa
þríhyrningsins er 7 cm?
e
Reiknaðu lengd hæðarinnar í þríhyrningunum í c-lið og d-lið.
Í þríhyrningi þar sem hornin eru 30°, 60° og 90° er lengd
langhliðarinnar tvöföld lengd styttri skammhliðarinnar.
Reiknaðu lengdir óþekktu hliðanna í þríhyrningnum.
Tillaga að lausn
Þar sem þetta er þríhyrningur með 30°, 60° og 90°
horn er lengd langhliðarinnar tvöföld lengd styttri
skammhliðarinnar.
Við köllum styttri skammhliðina
x
. Þá er lengd
langhliðarinnar 2
x
.
Pýþagórasarreglan segir:
langhlið
2
= skammhlið
1
2
+ skammhlið
2
2
(2
x
)
2
= 9
2
+
x
2
4
x
2
− x
2
= 9
2
3
x
2
= 81
x
2
=
81
___
3
x
2
= 27
x
= 27
x ≈ 5,2
2
x
≈ 10,4
Styttri skammhliðin er um það bil 5,2 m og langhliðin
er um það bil 10,4 m.
30°
60°
30°
60°
9 m
















