
Sýnidæmi 1
53
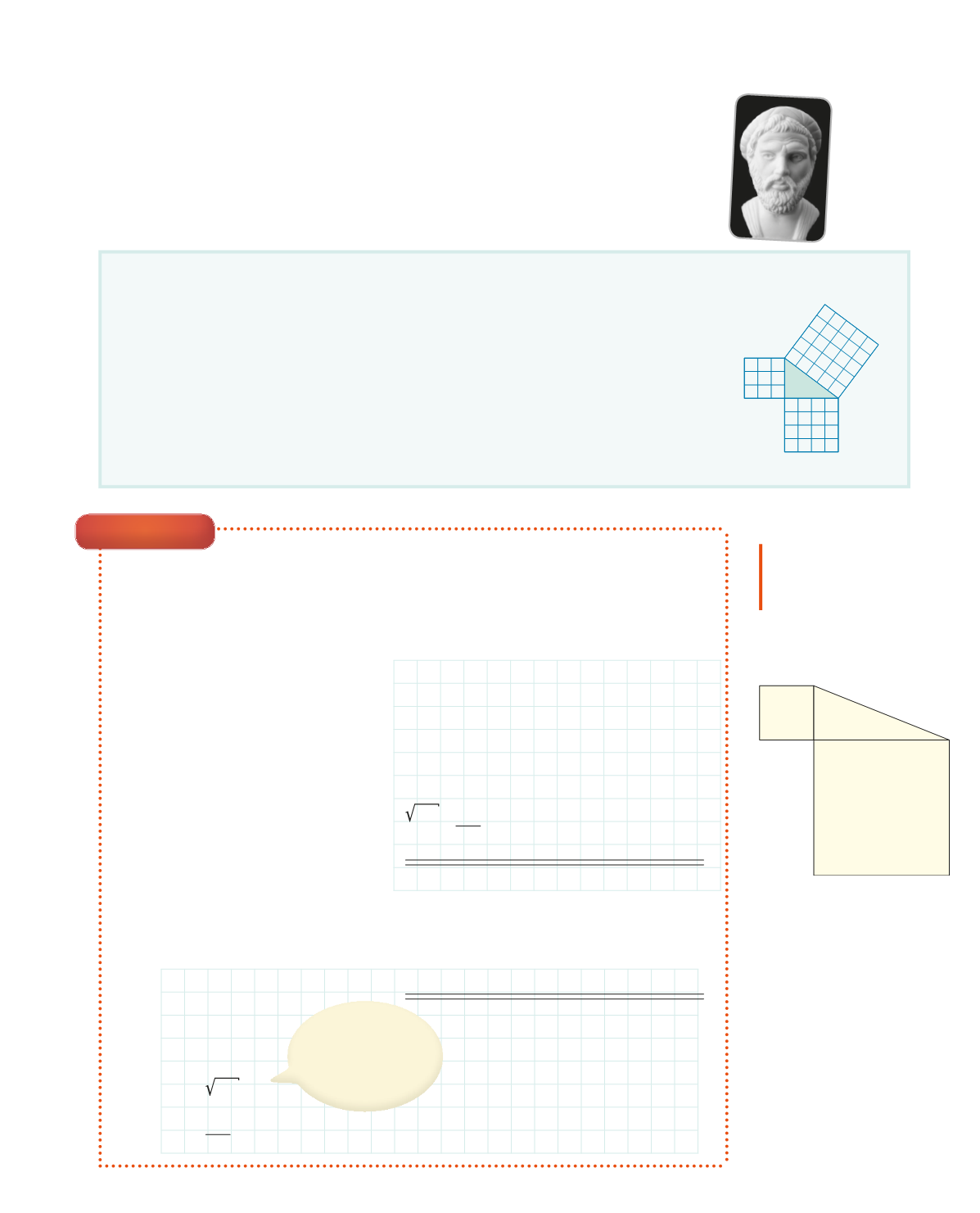
Regla Pýþagórasar
Í verkefninu á blaðsíðunni á undan komu í ljós tengsl sem rakin eru til stærð-
fræðingsins og heimspekingsins Pýþagórasar sem var uppi um það bil 550
f.Kr.Þessi tengsl kallast
Pýþagórasarregla
og hún er notuð þegar lengdir tveggja hliða
í rétthyrndum þríhyrningi eru þekktar og reikna á út lengd þriðju hliðarinnar.
Regla Pýþagórasar
Í rétthyrndum þríhyrningi er summa flatarmála ferninganna út frá
skammhliðunum tveimur jöfn flatarmáli ferningsins út frá langhliðinni.
langhlið
2
= skammhlið
1
2
+ skammhlið
2
2
Reglan gildir einnig í hina áttina. Ef summa flatarmála ferninganna
út frá skammhliðunum tveimur er jöfn flatarmáli fernings út frá
langhliðinni er þríhyrningurinn rétthyrndur.
Í rétthyrndum þríhyrningi eru skammhliðarnar 2 cm og 5 cm á lengd.
Finndu lengd langhliðarinnar.
Tillaga að lausn 1
Við teiknum þríhyrninginn og
notum ferningaaðferðina.
Við teiknum hjálparmynd og
skráum málin sem eru þekkt,
á hana. Síðan reiknum við
flatarmál ferninganna sem
eru út frá hliðunum sem
þekktar eru.
Tillaga að lausn 2
Við leysum dæmið langhlið
2
= skammhlið
1
2
+ skammhlið
2
2
l
2
= 2
2
+ 5
2
l
2
= 4 + 25
l
2
= 29
l
= 29
l
≈ 5,4
Venjulega
eru ekki notaðar
mælieiningar inn
í
jöfnum.
L S
1
S
2
2 cm
5 cm
25 cm
4 cm
Pýþagórasarregla
langhlið
2
=
skammhlið
1
2
+ skammhlið
2
2
Flatarmál ferningsins út frá langhliðinni:
(4 + 25) cm
2
= 29 cm
2
Ef við þekkjum flatarmál ferningsins
getum við fundið hliðarlengdina með
því að finna ferningsrót af flatarmálinu:
29 ≈ 5,4
Langhliðin er um það bil 5,4 cm á lengd.
Langhliðin er um það bil 5,4 cm á lengd.
















