
Kafli 3 • Algebra og jöfnur
147
Hvers vegna má bæta við, draga frá, margfalda og deila með sömu tölu báðum
megin við ójöfnumerkið?
1
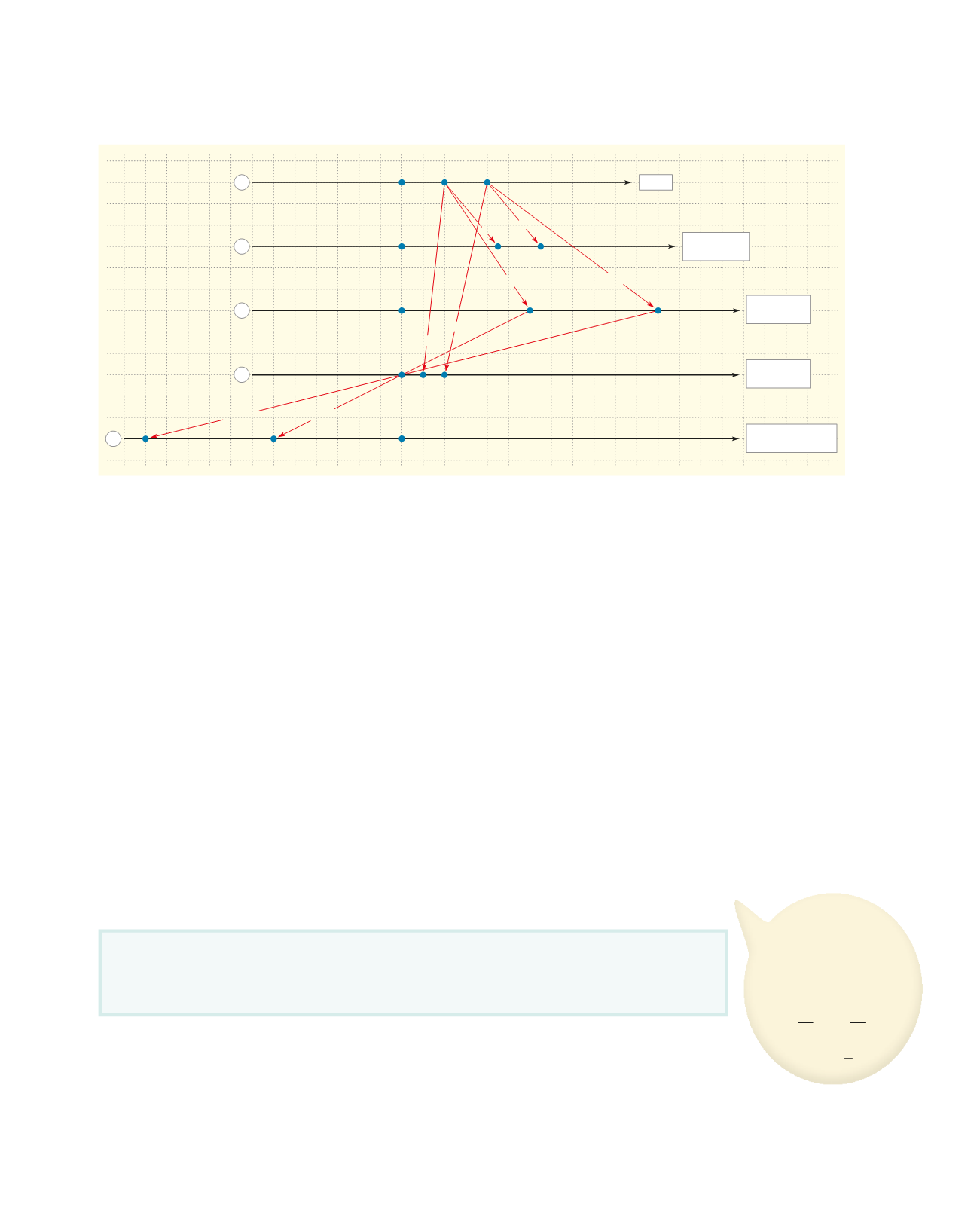
Á fyrstu talnalínunni hafa tölurnar 4 og 8 verið merktar. Tölurnar vinstra megin á
talnalínunni eru minni en þær sem eru til hægri þannig að 4 < 8.
2
Ef tölu er bætt við, til dæmis 5, flytjast báðar tölurnar fimm einingar til hægri
en röð þeirra innbyrðis breytist ekki. Á sama hátt flytjast tölurnar jafn mikið til
vinstri þegar tala er dregin frá.
3
Ef margfaldað er með jákvæðri tölu, til dæmis með 3, munu báðar tölurnar
þrefaldast en röð þeirra á talnalínunni helst óbreytt.
4
Sama gerist ef deilt er með jákvæðri tölu, til dæmis með 2.
5
En hvað gerist ef við margföldum með neikvæðri tölu?
Ef við til dæmis margföldun 12 með –1 og 24 með –1 sjáum við að röð
talnanna á talnalínunni breytist.
Þegar við margföldum með –1 speglast tölurnar um 0-punktinn þannig að talan
sem var lengra til vinstri lendir nú lengra til hægri á talnalínunni. Hér kemur í ljós
ný regla sem gildir um ójöfnur:
0
0
9
0
0
0
4
8
4 + 5
13
12
2 4
-12
-24
8 + 5
4 3
8 3
4 : 2
8 : 2
24 (-1)
12 (-1)
24
1
2
3
4
5
4 < 8
4 + 5 < 8 + 5
9 < 13
4 3 < 8 3
12 < 24
4 : 2 < 8 : 2
2 < 4
12 (-1) > 24 (-1)
-12 > -24
Þegar við margföldum eða deilum með neikvæðri tölu báðum megin
við ójöfnumerkið þarf að snúa ójöfnumerkinu við.
Að deila með
neikvæðri tölu
samsvarar því
að margfalda með
1 deilt með tölunni:
= 8
∙
8
–2
1
–2
= 8
∙
( – )
1
2
















