
Sýnidæmi 21
Kafli 3 • Algebra og jöfnur
139
Nú skulum við sjá hvernig mynstrið breytist ef við finnum ferningsstærð mismunar
í staðinn fyrir ferningsstærð summu.
Margfaldaðu upp úr svigunum.
a
(
x
− 1)
2
b
(
x
− 3)
2
c
(
a
+
b
)
2
Tillaga að lausn
a
(
x
− 1)
2
= (
x
− 1)(
x
− 1) =
x
2
−
x
−
x
+ 1 =
x
2
− 2
x
+ 1
b
(
x
− 3)
2
= (
x
− 3)(
x
− 3) =
x
2
− 3
x
− 3
x
+ 9 =
x
2
− 6
x
+ 9
c
(
a
−
b
)
2
= (
a
−
b
)(
a
−
b
) =
a
2
−
ab
−
ab
+
b
2
=
a
2
− 2
ab
+
b
2
Í þessu sýnidæmi höfum við reiknað út ferningsstærð mismunar milli
tveggja liða. Hér þarftu líka að skoða mynstrið í svörunum og læra að
skrifa svar án milliútreiknings.
Eini munurinn á sýnidæmunum með ferningsstærð summu og
ferningsstærð mismunar er að liðurinn í miðjunni í svarinu er
neikvæður. Það merkir að ferningsstærð mismunar milli tveggja liða
er jöfn ferningsstærð fyrri liðarins mínus tvöfalt margfeldi beggja liða,
plús ferningsstærð síðari liðarins. Þetta er
önnur ferningsreglan.
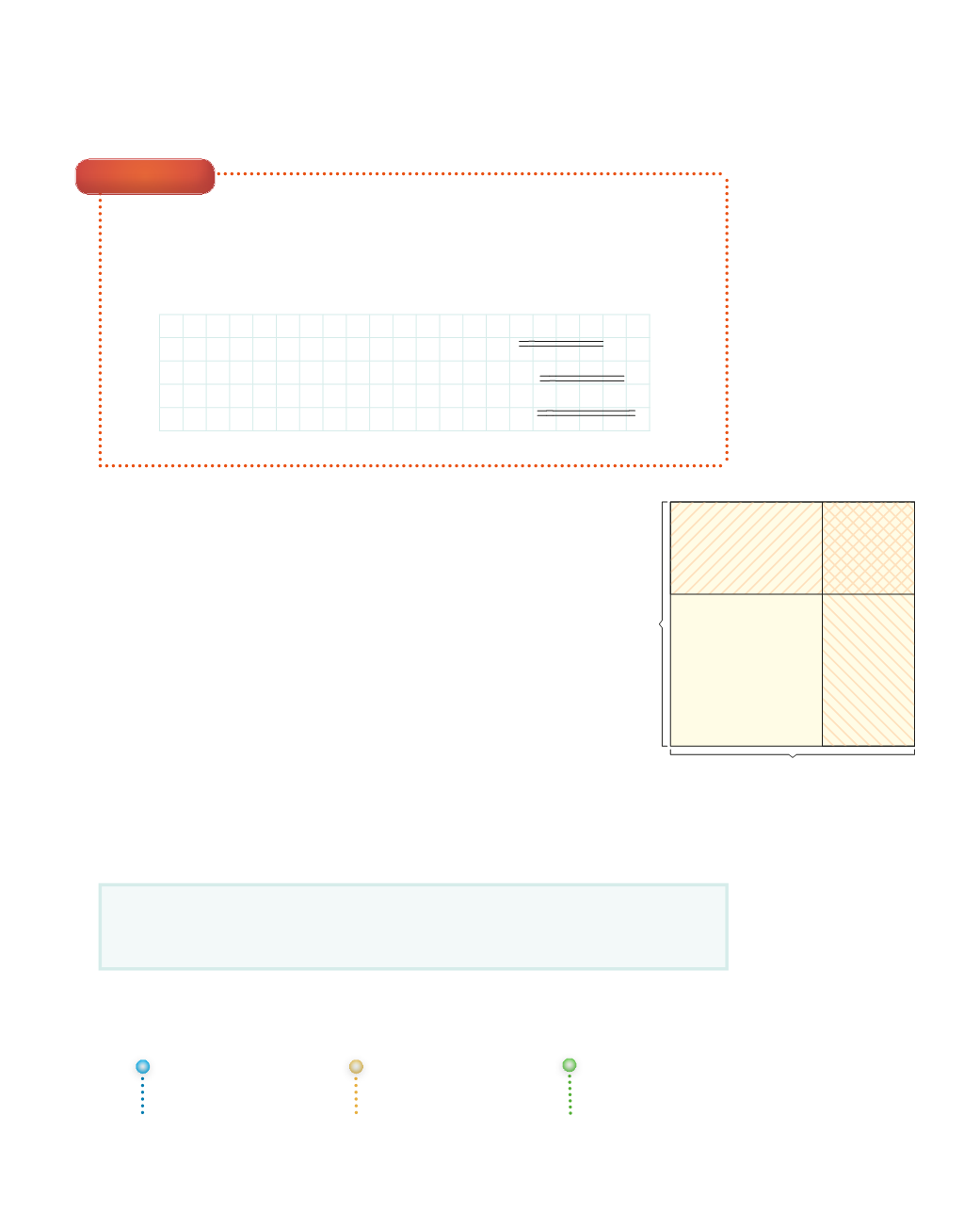
Aðra ferningsregluna
má einnig sýna með rúmfræðimynd. Stærri innri
ferningurinn hefur flatarmálið
(a − b)
2
. Flatarmál stóra ferningsins er
a
2
. Ef við drögum flatarmál efri rétthyrningsins (með flatarmálið
ab
)
og rétthyrningsins til hægri (einnig með flatarmálið
ab
) frá stóra rétthyrningnum,
það er að segja
a
2
− 2ab
, höfum við dregið flatarmál ferningsins með hliðina b
tvisvar frá. Þá verðum við að bæta
b
2
við til að fá flatarmálið
(a − b)
2
.
Önnur ferningsreglan
(
a
−
b
)
2
=
a
2
− 2
ab
+
b
2
3.50
Notaðu
aðra ferningsregluna
til að skrá svörin án milliútreiknings.
a
(
x
− 8)
2
b
(
b
− 5)
2
c
(3
a
− 1)
2
d
(4
−
x
)
2
e
(2
a
− 3
b
)
2
f
(
x
−
1
___
2
)
2
b
b
b
b
a b
a b
(a b)
a
a
















