
Skali 3A
132
Margföldun stæða innan sviga
Þegar þú átt að margfalda liðastærð innan sviga með tölu eða bókstafastæðu þarf
að margfalda alla liði í sviganum með tölunni eða bókstafastæðunni. Þannig eyðir
þú sviganum:
2
a
(
b
− 3
ab
) = 2
a
·
b
−2
a
· 3
ab
= 2
ab
− 6
a
2
b
Þú getur sleppt milliútreikningnum þegar þú getur fundið margfeldið með
hugareikningi. Þegar margfalda á saman tvo sviga getur þú fyrst hugsað þannig að
seinni sviginn sé bókstafastæða sem á að margfalda með liðunum í fyrri sviganum.
Þá ferðu að eins og hér fyrir ofan til að eyða síðari sviganum.
(
a
+ 3
b
)(2
a
+
b
) =
a
· (2
a
+
b
) + 3
b
· (2
a
+
b
) =
a
· 2
a
+
a · b
+ 3
b
· 2
a
+ 3
b
·
b
=
2
a
2
+
ab
+ 6
ab
+ 3
b
2
=
2
a
2
+ 7
ab
+ 3
b
2
Þú getur hoppað beint frá fyrstu línu til næstsíðustu línu ef þú hugsar þér að
margfalda eigi inn í svigann (2
a
+
b
) með a og þar næst eigi að margfalda inn í
svigann (2
a
+
b
) með 3b.
Þetta má sýna á þennan hátt: (
a
+
b
)(
c
+
d
) =
ac
+
ad
+
bc
+
bd
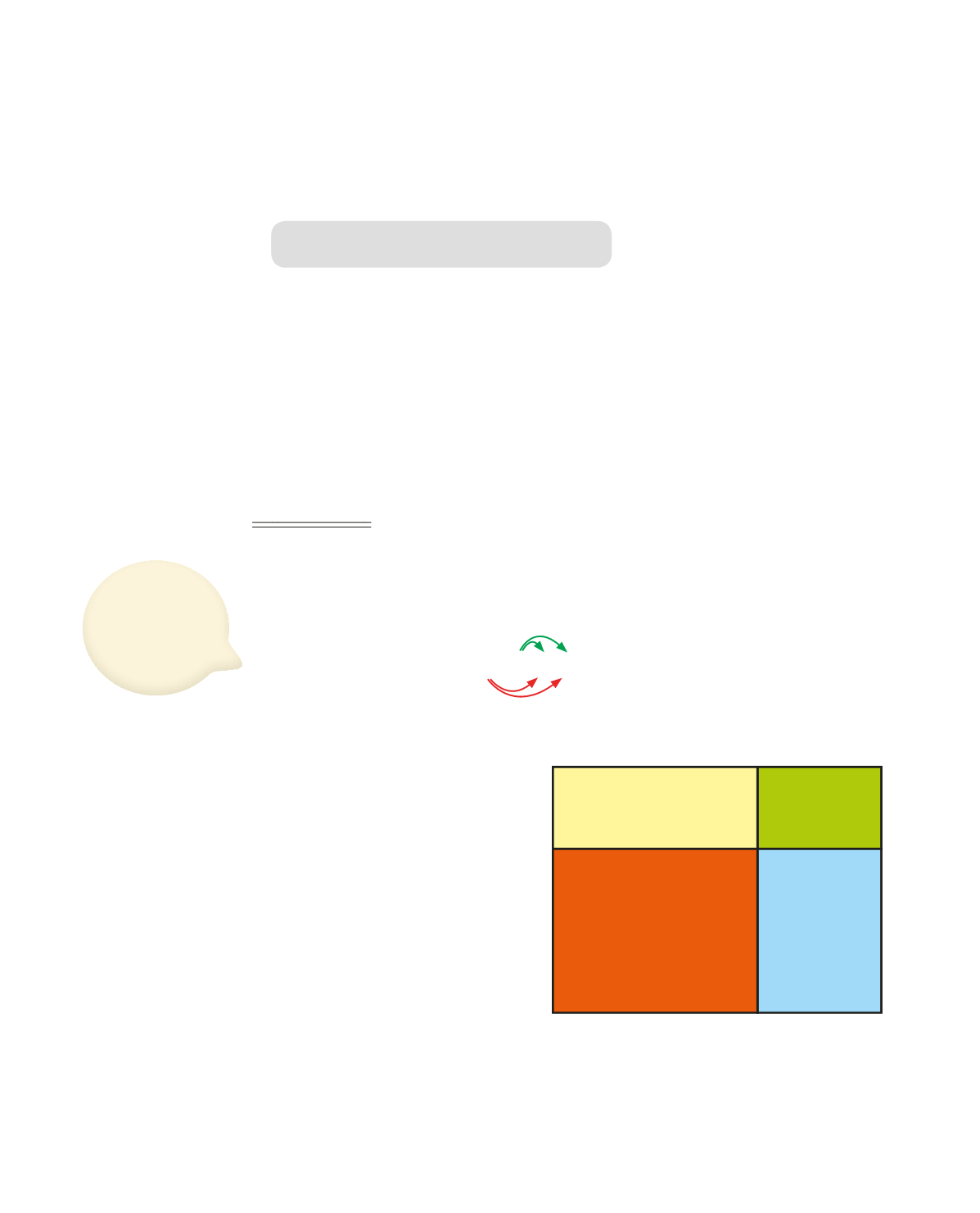
Þetta má einnig sýna með
rúmfræðimynd þar sem flatarmál
rétthyrninga er skoðað.
Flatarmál stóra rétthyrningsins
er (
a
+
b
)(
c
+
d
) en það er
einmitt summan af minni
rétthyrningunum fjórum, þeim
rauða, gula, bláa og græna.
ad
d
c
ac
bd
bc
a
b
Ef mínus
er í öðrum
sviganum þarftu
að muna eftir
formerkjunum.
















