
Sýnidæmi 14
Skali 3A
128
Í bókstafastæðu er gott að athuga fyrst hvort hægt sé að þátta og stytta. Þú skalt
ekki margfalda saman bókstafastæður strax í upphafi. Mundu að ef fleiri en einn
liður er í einhverju almenna brotinu verðurðu að setja sviga utan um liðastærðirnar
áður en þú setur brotin upp á eitt strik.
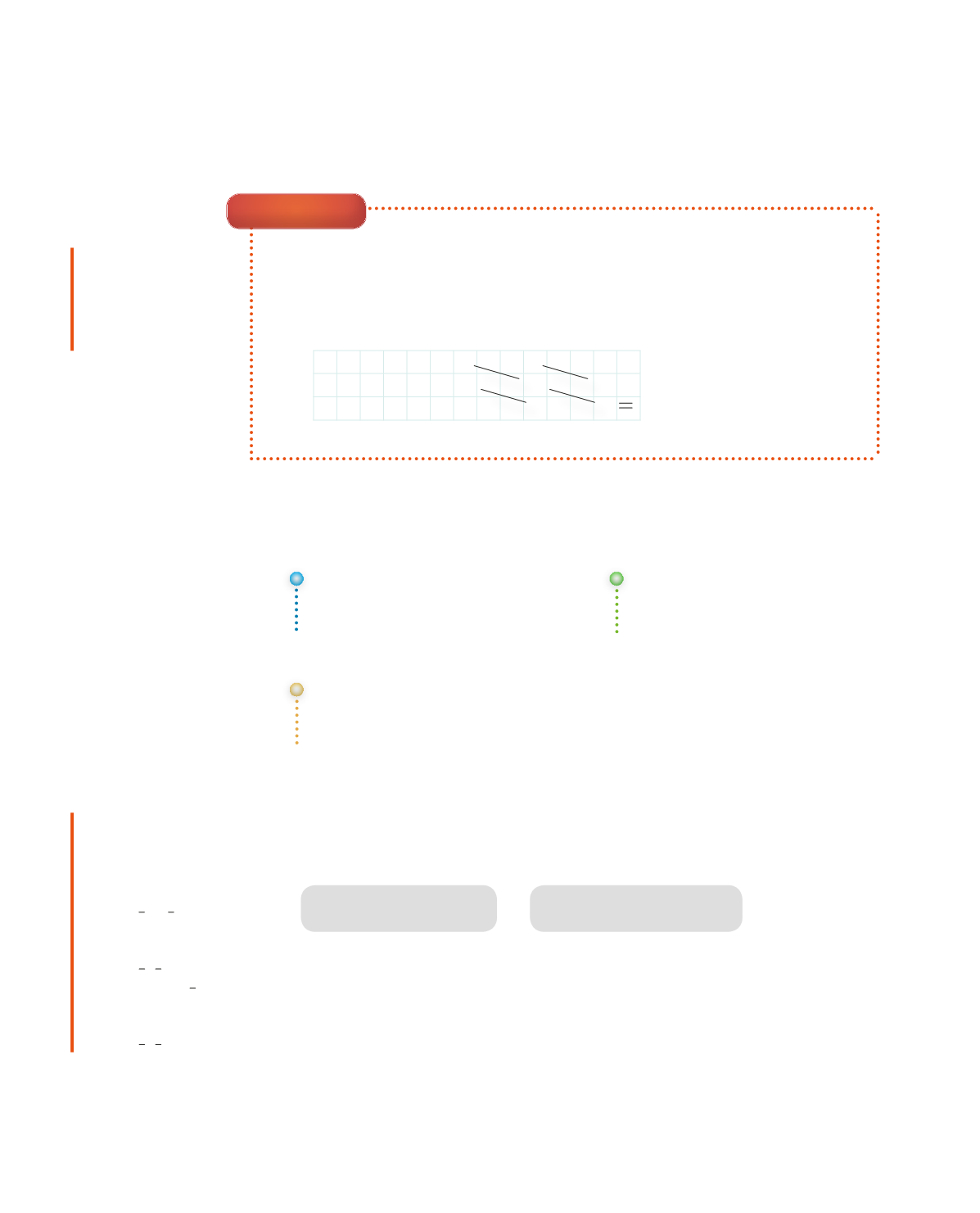
Þáttaðu og styttu ef hægt er. Fullstyttu almenna brotið í svarinu.
x
− 2
_______
3
x
+ 3
∙
x
2
+
x
_______
2
x
− 4
Tillaga að lausn
x
− 2
_______
3
x
+ 3
∙
x
2
+
x
_______
2
x
− 4
=
(
x
− 2) ·
x
(
x
+ 1)
_________________
3(
x
+ 1) · 2(
x
− 2)
=
x
___
6
3.33
Þáttaðu og styttu þar sem hægt er.
Fullstyttu brotið í svarinu.
a
x
___
3 ∙
9
____
4
x
b
2
a
+ 4
_______
5
·
5
a
______
a
+ 2
c
x
______
2 −
x
·
4
y
− 2
xy
_________
x
2
d
a
2
+ 2
_______
ab
·
a
2
b
2
_________
10 + 5
a
2
e
xy
2
−
x
2
y
_________
4
x
− 2
·
2
x
2
−
x
_________
x
2
y
−
xy
2
f
a
2
− 2
ab
_________
b
2
+
b
·
b
2
+
b
3
_________
ab
− 2
b
2
Þegar deilirinn í deilingardæmi er almennt brot geturðu fundið svarið með því
að breyta stæðunni í margföldunardæmi með
margföldunarandhverfu
brotsins.
Þá skipta teljari og nefnari um sæti.
4 :
2
___
3
= 4 ·
3
___
2
=
4 · 3
_____
2
= 6
3
___
8
:
3
___
4
=
3
___
8
·
4
___
3
=
3 · 4
_____
8 · 3
=
1
___
2
Þegar brotið inniheldur bókstafastæðu ferðu nákvæmlega eins að. Eftir að þú hefur
snúið við brotinu sem deilt er með og sett margföldunarmerki í stað deilingarmerkis
þarftu að þátta og stytta eins og hægt er. Það er nákvæmlega eins og þegar þú
reiknar með tölum.
Liðastærð
er stærð
sem skiptist í liði,
t.d. 8 + x,
a – b + x,
3x – 8
4(x
2
) + 3
∙
4
Margföldunar-
andhverfa
er brotið
sem tala er marg-
földuð með til að
fá margfeldið 1.
T.d. eru
2
3
og
3
2
margföldunar-
andhverfur vegna
þess að
2
3
∙
3
2
= 1.
Einnig eru 6 og
1
6
margföldunar-
andhverfur vegna
þess að
6
1
∙
1
6
= 1.
1
1
1
1
















