
Sýnidæmi 4
Kafli 3 • Algebra og jöfnur
113
Leystu jöfnuhneppið með því að teikna gröf jafnanna.
I
x
+ 5
y
= 10
II
3
x
−
y
= 14
Tillaga að lausn
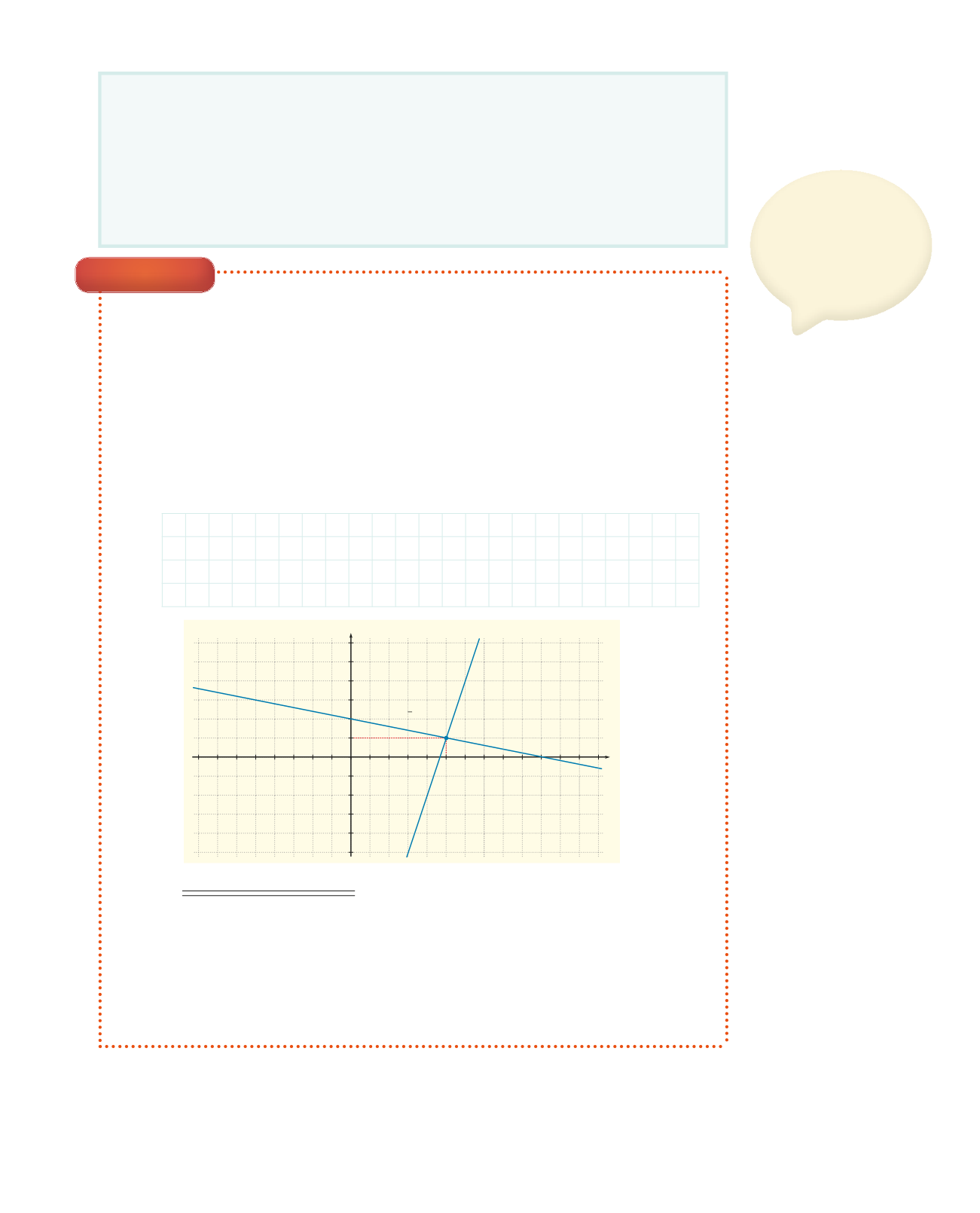
Teikning í höndunum:
Ef við leysum jöfnuhneppið með tilliti til x með því að teikna
gröf jafnanna er hagkvæmast að gera það þannig að við sjáum
hallatölurnar og skurðpunktana við y-ásinn..
I
x +
5
y
= 10
5
y
= −
x
+ 10 | : 5
y
= −
1
___
5
x
+ 2
Lausnin:
x
= 5 og
y
= 1
Stafræn teikning:
Við leysum jöfnuhneppið með rúmfræðiforriti og teiknum gröf
jafnanna. Við skráum hvora jöfnu í inntaksreitinn og ýtum á
færsluhnappinn („enter“-hnappinn). Þá birtast gröfin og hægt er að
lesa hnit skurðpunktsins.
3.11
Leystu dæmi 3.4 og 3.6 með því að teikna gröf jafnanna. Gakktu úr skugga
um að þú fáir sömu lausn og þegar þú leystir jöfnuhneppin með reikningi.
Þegar um
jöfnuhneppi
er að ræða má sýna
hvora jöfnuna fyrir sig
sem beina línu í
hnitakerfi.
Grafísk lausn
Hægt er að leysa línulegt jöfnuhneppi með teikningu. Hvora jöfnu
má tákna með beinni línu eða grafi og við teiknum línurnar í sama
hnitakerfi. Ef línurnar skerast hefur jöfnuhneppið lausn. Það er
x-gildið og y-gildið sem er lausn í báðum jöfnunum, nefnilega hnit
skurðpunktsins.
7 8 9 10 11 12 13
y
= 3
x
− 14
Skurðpunkturinn (5, 1)
sýnir að lausnin er
x
= 5 og
y
=1
y
= –
x
+ 2
1
5
5
4
3
2
1
–1
–2
–4 –3 –2 –1 0
0
1 2 3 4
y
−ás
x
−ás
5 6
6
–5 –6
–3
–4
–5
–7 –8
II
3
x
−
y
= 14
−
y
= − 3
x
+ 14 | : − 1
y
= 3
x
− 14
















