
Skali 3A
108
Jöfnur með fleiri en einni óþekktri stærð
Þegar fleiri en ein óþekkt stærð er í jöfnu geta margar lausnir komið til greina.
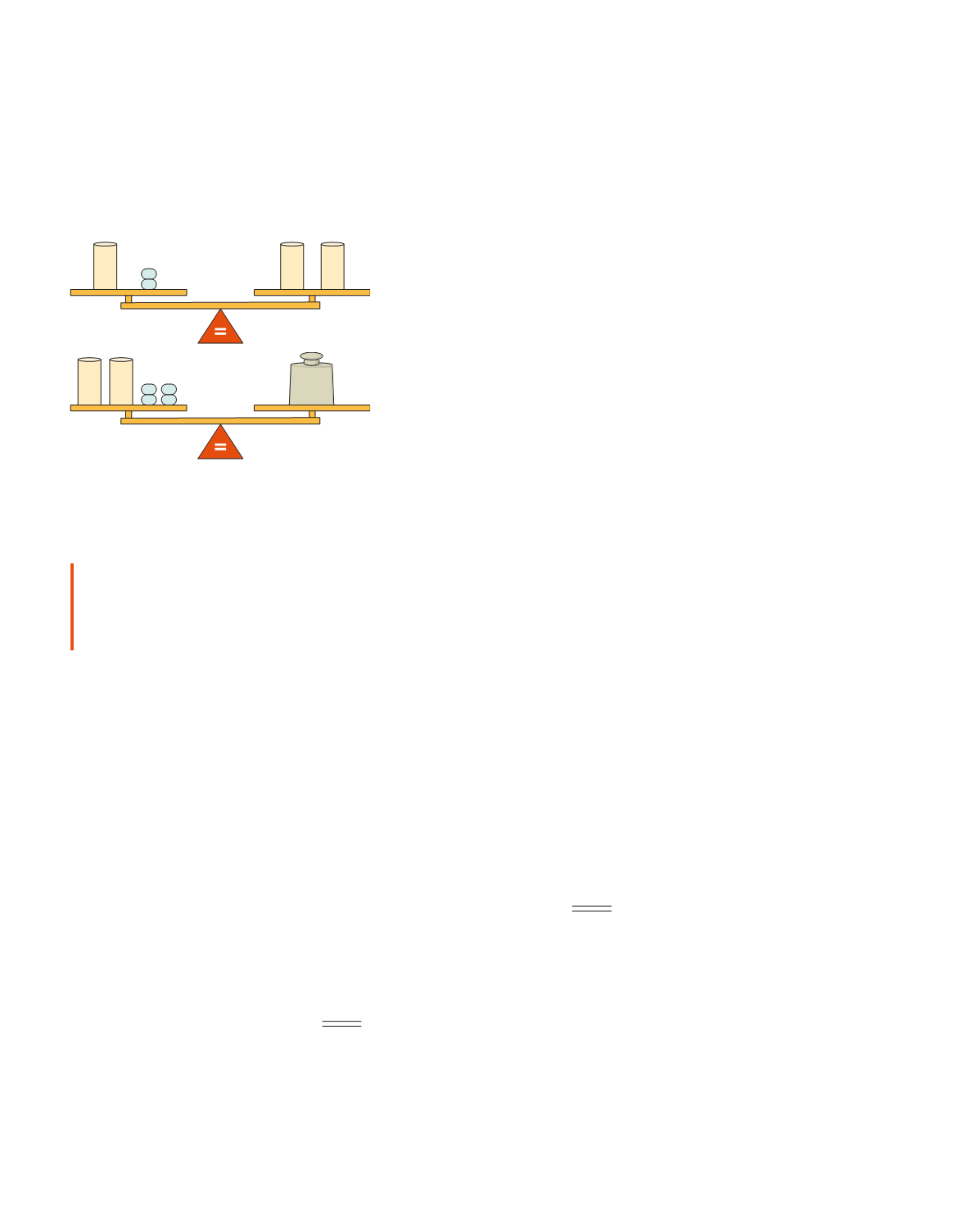
Ef vogin á mynd 1 er í jafnvægi má segja að sívalningur hafi sama gildi og tvær
kúlur en við vitum ekki hvert gildi kúlnanna er. Það getur verið hvað sem er svo
fremi að sívalningurinn hafi tvöfalt gildi einnar kúlu.
Ef við eigum að finna gildi kúlunnar og sívalningsins þurfum
við meiri upplýsingar. Með þeim upplýsingum sem við höfum
fengið til viðbótar á mynd 2 getum við með rökhugsun fundið
lausn. Við sjáum að einn sívalningur og tvær kúlur vega
helminginn af 24 kg, það er að segja 12 kg. Af fyrri
upplýsingum má sjá að tveir sívalningar vega 12 kg og að
einn sívalningur vegur þá 6 kg. Þar með vegur ein kúla 3 kg.
Þetta má setja fram sem tvær jöfnur. Látum
x
tákna þyngd
sívalnings og
y
þyngd kúlu.
Mynd 1 gefur jöfnuna:
I
x
+ 2
y
= 2
x
Mynd 2 gefur jöfnuna:
II
2
x
+ 4
y
= 24
Leysa má
jöfnuhneppi
á marga vegu. Í báðum jöfnunum hafa
x
og y sama gildi. Það
þýðir að við getum úr fyrri jöfnunni fundið stæðu sem táknar
x
og sett hana inn í
síðari jöfnuna. Þá höfum við minnkað dæmið niður í eina jöfnu með aðeins einni
óþekktri stærð og slíkar jöfnur hefur þú leyst áður. Í jöfnu II má deila með 2 báðum
megin við jöfnumerkið.
Jöfnurnar tvær má því umrita þannig:
I
2
y
= 2
x
−
x
2
y
=
x
II
x
+ 2
y
= 12
Af jöfnu I sérðu að setja má x í staðinn fyrir 2y. Jafna II verður þá
II
x
+
x
= 12
2
x
= 12
sem hefur lausnina
x
= 6
Ef við setjum lausnina inn í jöfnu I fæst:
2
y
= 6
y
= 3
Þetta er nákvæmlega það sama og við fengum með rökhugsuninni sem við
beittum á myndirnar af sívalningunum og kúlunum. Aðferðin sem notuð var
til að leysa þetta jöfnuhneppi kallast
innsetningaraðferðin
.
24 kg
Figur 1
Figur 2
Jöfnuhneppi
felur í sér tvær
eða fleiri jöfnur
með tvær eða fleiri
óþekktar stærðir.
















