
Markmið
Skali 3A
106
Línulegar jöfnur og
línuleg jöfnuheppni
HÉR ÁTTU AÐ LÆRA AÐ
• leysa línuleg jöfnuhneppi með innsetningaraðferðinni
• leysa línuleg jöfnuhneppi með samlagningaraðferðinni
• leysa línuleg jöfnuhneppi með teikniaðferðinni
• setja upp og leysa línuleg jöfnuhneppi sem tengjast daglegu lífi
• reikna með formúlum
Jafna er samsett úr tveimur stæðum sem tengdar eru með jöfnumerki. Það
þýðir að stæðurnar eru jafngildar. Jafna inniheldur eina eða fleiri óþekktar stærðir.
Það sem stendur vinstra megin við jöfnumerkið er jafnt því sem stendur hægra
megin
. Jöfnurnar sem þú hefur leyst fram að þessu hafa haft eina óþekkta stærð.
Venjulega er bókstafurinn
x
notaður til að tákna óþekktu stærðina og þú hefur
lært hvernig leysa má slíkar jöfnur. Lausn jöfnu segir til um hvaða gildi
x
hlýtur
að hafa til að jafnan sé rétt.
Þú getur hugsað þér að jafna sé skálavog.
Það þarf að vera jafnvægi milli þess
sem er hægra megin og vinstra megin í jöfnunni
. Ef þú bætir við eða dregur frá
öðrum megin í jöfnunni verður þú að gera hið sama hinum megin. Sama á við um
margföldun og deilingu með tölum. Á meðan þú gætir þess að gera sömu
reikningsaðgerðirnar báðum megin mun jafnan verða áfram rétt. Þetta má sýna
með eftirfarandi mynd.
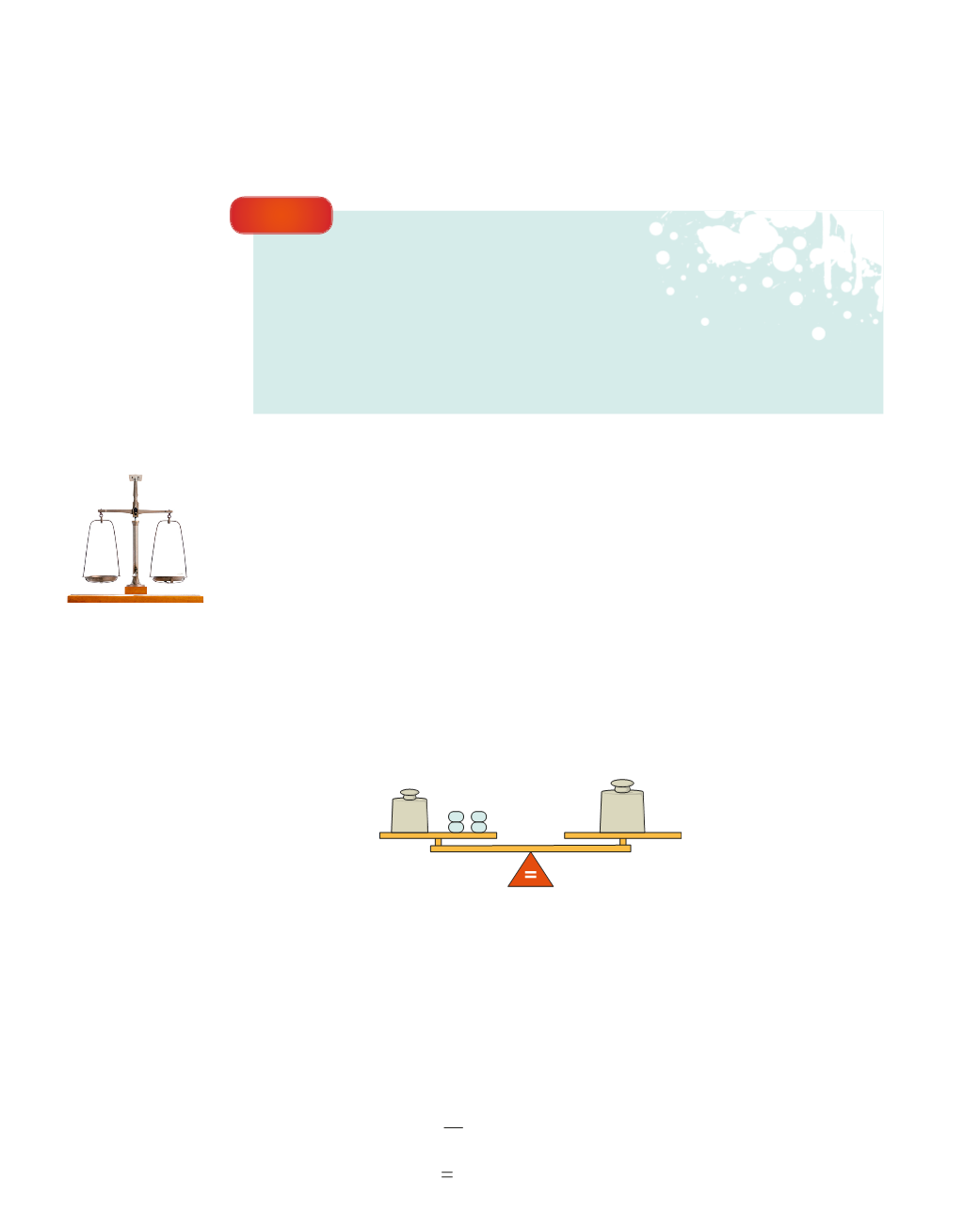
Fjórar jafn þungar kúlur plús 10 kg vega 26 kg. Ef við fjarlægjum 10 kg af hvorri
hlið sjáum við að fjórar kúlur vega 16 kg. Það þýðir að hver kúla vegur fjórðung af
16 kg, það er að segja 4 kg.
Láttu
x
tákna þyngd einnar kúlu í kílógrömmum. Með jöfnu verður þetta
sett þannig fram:
4
x
+ 10 = 26 | −10
4
x
= 16 | : 4
x
=
16
4
x
= 4
26 kg
10 kg
















