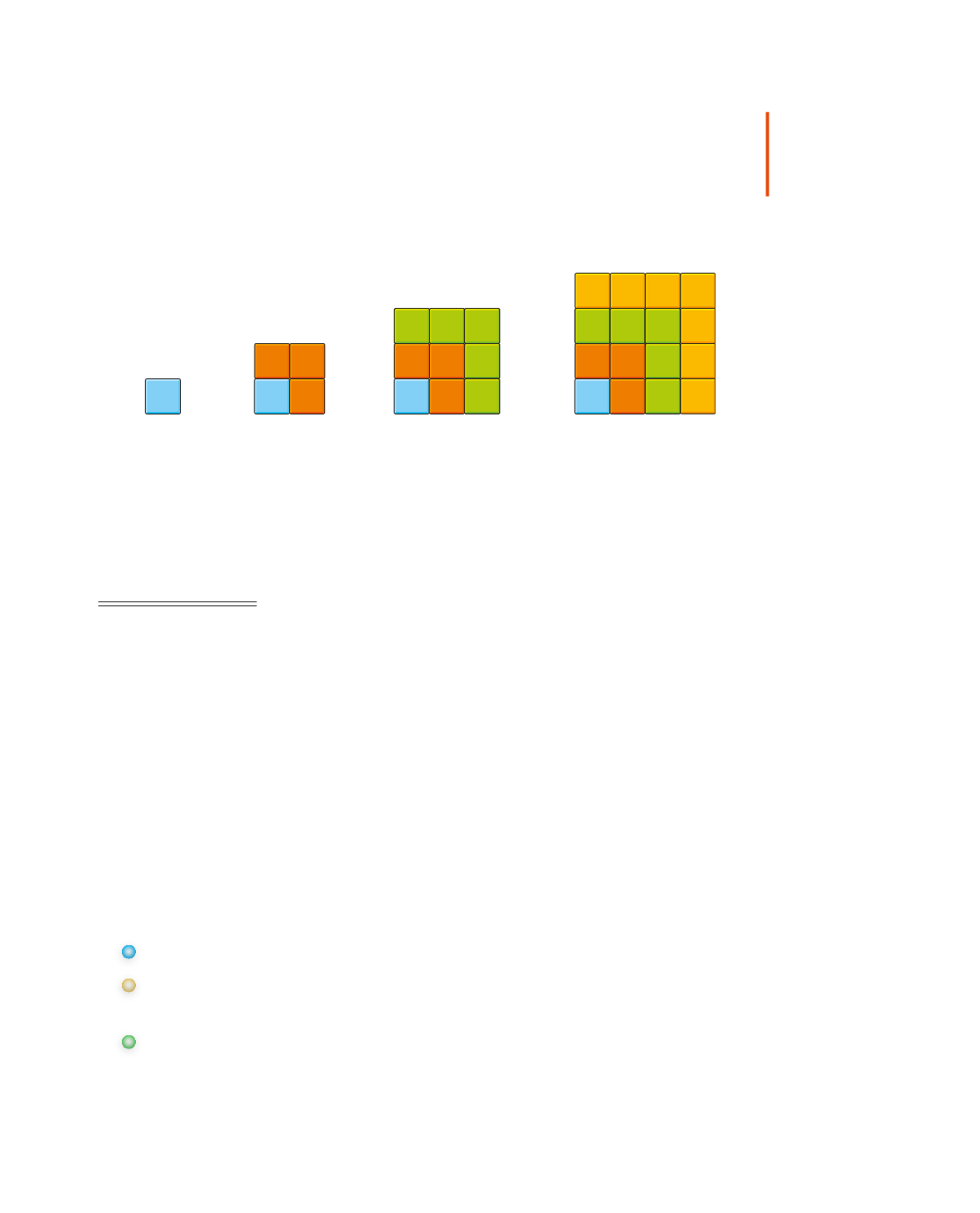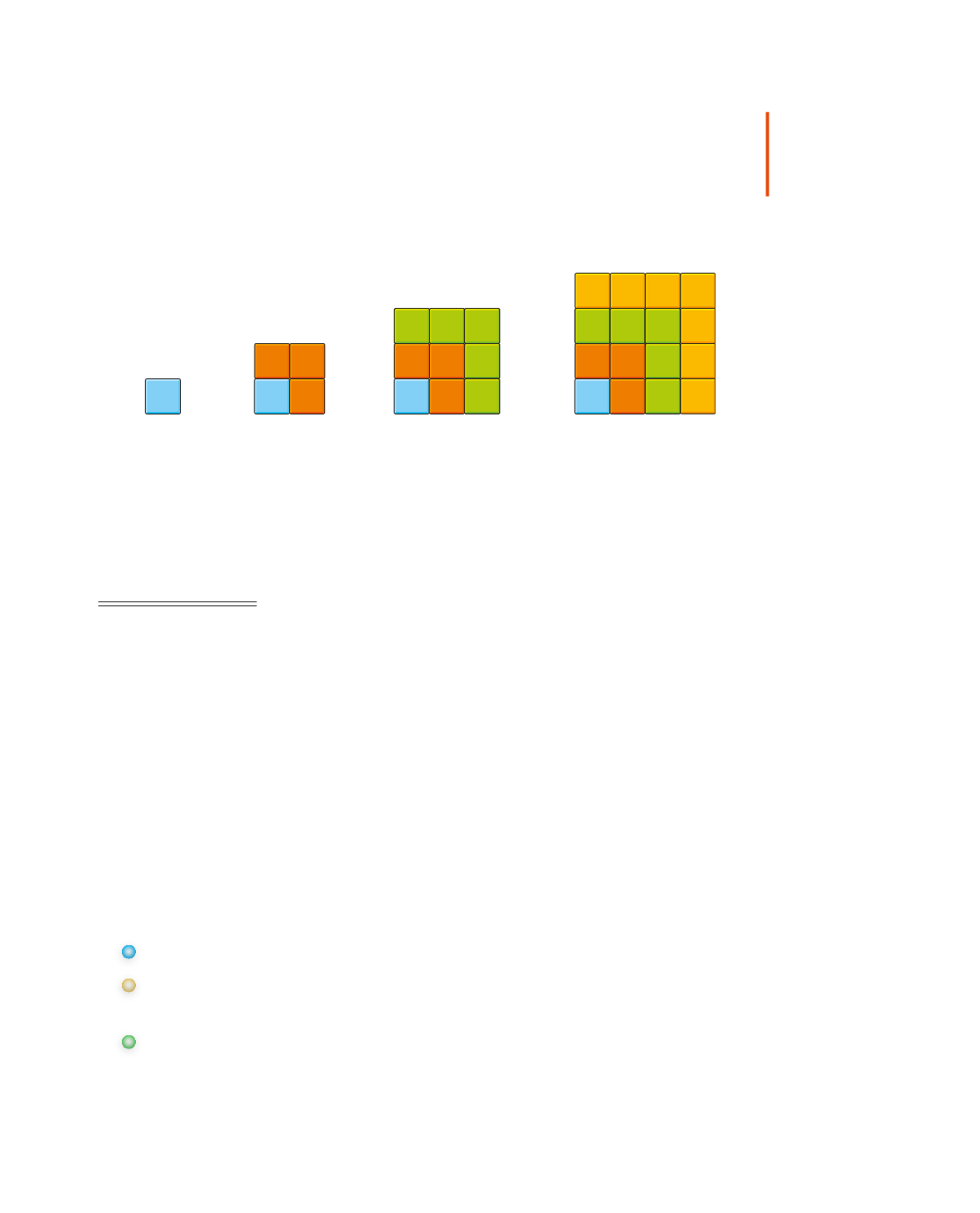
Rakningarformúla
Formúla sem gefur
myndtöluna út frá
fyrri myndtölu
í mynstrinu.
Kafli 5 • Algebra og jöfnur
75
Á bls. 280 er sýnt hvernig hægt er að finna fjölda kubba í hverjum ferningi með
beinni formúlu. Einnig er hægt að nota
rakningarformúlu
. Ferning má stækka með
því að bæta við hann þeim fjölda kubba sem er oddatala, þannig:
Mynd 1 hefur myndtöluna m
1
= 1
Mynd 2 hefur myndtöluna m
2
= 1 +
3
= m
1
+
3
= m
1
+ (
4
−
1
) = 4
Mynd 3 hefur myndtöluna m
3
= 4 +
5
= m
2
+
5
= m
2
+ (
6
−
1
) = 9
Mynd 4 hefur myndtöluna m
4
= 9 +
7
= m
3
+
7
= m
3
+ (
8
−
1
) = 16
Mynd 1
Mynd 2
Mynd 3
Mynd 4
Þegar þú átt til dæmis að reikna út m
3
reiknar þú 4 +
5
. Oddatalan 5 er jafnt og
6 − 1 = 2 · 3 − 1, það er einum minna en tvisvar sinnum 3. Til að finna m
4
þarftu að
leggja við 7 = 8 − 1 þannig að þetta passar. Þú átt sem sagt að taka fyrri myndtölu
og leggja við oddatöluna sem er einum minni en tvisvar sinnum myndtalan.
m
n
= m
n
— 1
+ (
2
n
−
1
)
2
n
− 1 er talan sem kemur á undan 2
n
af því að 2
n
− 1 er einum minni en 2
n
. Ef
n
er t.d. 17 þá er 2
n
− 1 = 33.
Þegar þú reiknar með rakningarformúlu þarftu að reikna út allar myndtölurnar frá
m
1
og áfram alveg þangað til þú ert komin að þeirri myndtölu sem þú vilt finna.
5.10
Notaðu myndirnar í verkefni 5.9.
a
Útskýrðu hvernig þú getur fundið hve margir kubbar eru í mynd 5 þegar
þú veist hve margir kubbar eru í myndinni á undan.
b
Sýndu − með því að teikna eða nota kubba − að aðferðin, sem þú fannst
í a-lið, eigi við mynd 4 og 5.
c
Hve marga kubba þarf Elísa til að búa til allar fimm fyrstu myndirnar?
d
Búðu til rakningarformúlu fyrir m
n
út frá því sem þú fannst í a-lið.
Sýndu að formúlurnar passa við m
6
og m
7
.
e
Elísa hefur 100 kubba. Hún ætlar að búa til eins margar myndir og hægt
er frá mynd 1 og áfram.
Hve margar fullgerðar myndir getur hún búið til?
Verða einhverjir kubbar afgangs?